Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Движение по вертикали
Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с^2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8
м/с2.
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
FAQ (скорость):
Как вы рассчитываете скорость (с примером)?
Чтобы вычислить скорость, вы должны разделить расстояние на время, которое требуется, чтобы пройти то же самое расстояние, совсем на следующем, вы должны добавить к нему свое направление. Наш скоростной искатель также определяет скорость таким же образом.
Например:
Если вы проехали 50 миль в течение 1 часа, двигаясь на запад, то говорят, что ваша скорость составляет 50 миль в час на запад или 50 миль в час на запад.
Как вы находите скорость с расстоянием и временем?
Все, что вам нужно, чтобы вставить значения в вышеупомянутый калькулятор скорости и времени, чтобы найти скорость с расстоянием и временем.
- Прежде всего, вы должны нажать на «вкладку ускорения»
- Совсем скоро вы должны выбрать опцию «конечная скорость» из выпадающего меню финала конвертер скорости
- Затем вы должны ввести значение начальной скорости в указанное поле
- Сразу после этого вы должны ввести значение ускорения в данное поле
Наконец, вы должны ввести значение времени в указанное поле, затем, нажав кнопку «Рассчитать», калькулятор окончательной скорости мгновенно вычислит конечную скорость для заданных входных данных.
Может ли скорость быть отрицательной?
Непосредственно – да, скорость может быть отрицательной. Объект, который движется в отрицательном направлении, обозначен как отрицательная скорость. И, если объект ускоряется, то его ускорение – это то, что направлено в том же направлении, что и его движение (в таком случае это называется отрицательным ускорением).
Как найти начальную скорость?
Если вы хотите мгновенно рассчитать начальную скорость, то все, что вам нужно, это вставить значения в вышеуказанную начальную конвертер скорости. И, если вы хотите сделать это вручную, используйте приведенную ниже формулу начальной скорости:
Начальная формула скорости:
Начальная скорость = конечная скорость – (ускорение × время)
vi = vf – в
Читай дальше!
Прежде всего, вы должны выяснить, какое из смещения (S), конечной скорости (Vf), ускорения (A) и времени (T) вы должны решить для начальной скорости (vi)
- Если у вас есть Vf, A и T, то вы должны использовать Vi = Vf – AT
- Если у вас есть S, Vf и T, то вы должны использовать Vi = 2 (S / T) – Vf
- Если у вас есть S, Vf и A, то вы должны использовать Vi = квадратный корень из (Vf ^ 2 – 2AS)
- Если у вас есть S, A и T, то вы должны использовать Vi = (S / T) – (AT / 2)
Как найти конечную скорость?
Попробуйте приведенный выше финал калькулятор скорости, чтобы выполнить мгновенные вычисления. Если вы хотите сделать это самостоятельно, то вам следует использовать данную формулу окончательной скорости.
V = U + AT
S = UT + 1/2 AT ^ 2
V ^ 2 = U ^ 2 + 2AS
Читай дальше!
Прежде всего, выясните, какую из начальной скорости (U), времени ускорения (A) (T) и смещения (S) вы должны решить для конечной скорости.
- Если у вас есть U, A и T, то вы должны использовать V = U + AT
- Если у вас есть S, U и T, то вам следует попробовать V = 2 (S / T) – U
- Если у вас есть S, U и A, то вы должны использовать V = квадратный корень (U ^ 2 + 2AS)
- Если у вас есть S, A и T, то вы должны использовать V = (S / T) + (AT / 2)
Что вызывает изменение скорости?
Эксперты изображают, что силы – это то, что влияет на движение объектов – они могут вызывать движение, также они могут останавливаться, замедляться или даже изменять направление движения объекта калькулятор скорости. Поскольку сила вызывает изменения в скорости или направлении объекта, говорят, что силы вызывают изменения в скорости. Помните, что ускорение называется изменением скорости.
Конец Примечание:
Имейте в виду, что скорость зависит от расстояния, а когда речь идет о скорости, она зависит от смещения – несомненно, эти две величины фактически одинаковы (даже имеют одинаковую величину), когда интервал времени мал. Используйте вышеупомянутый инструмент, чтобы понять, как вычислить скорость и даже решить ваши физические уравнения в мгновение ока!
Other Languages: Velocity Calculator, Hız Hesaplama, Kalkulator Prędkości, Geschwindigkeit Berechnen, 時速計算, Výpočet Rychlosti, Calculo De Velocidade, Calcul Vitesse, Calcular Velocidad, Calcolo Velocità, 속도 계산기, Kalkulator Kecepatan, حاسبة السرعة, Nopeuslaskin
От чего зависит тормозной путь?
Очевидно, что дистанция торможения будет различной в зависимости от ситуации и ее условий. Так, факторы, влияющие на величину этого пути, делят на две группы:
- Факторы, которые зависят от автомобилиста.
- Факторы, которые не зависят от автомобилиста.
К условиям, которые не зависят от того, кто управляет автомобилем, относят погоду и состояние дорожного покрытия. Что касается погоды, то логично, что в дождь, снег или гололед времени для остановки машины потребуется больше, чем в сухую погоду.
 Дорожное покрытие тоже оказывает влияние на расстояние торможения. Если дорога гладкая без добавления камня, то дистанция, которая будет пройдена транспортным средством при торможении, также будет больше.
Дорожное покрытие тоже оказывает влияние на расстояние торможения. Если дорога гладкая без добавления камня, то дистанция, которая будет пройдена транспортным средством при торможении, также будет больше.
Гораздо больше факторов, которые зависят от водителя (владельца машины):
скорость. Логично, чем меньше скорость, тем короче расстояние торможения;
состояние и устройство тормозной системы
Важно, чтобы машина, в том числе ее тормоза, работала исправно, чтобы колодки не были изношены, а давление в шинах было достаточным.
вид установленных шин. Протектор не должен быть сильно изношен, а тип установленной резины должен соответствовать погодным условиям;
загрузка автомобиля
Чем легче транспортное средство, тем проще его остановить. Расстояние торможения нагруженного автомобиля будет более длинным;
наличие системы ABS. На сухом асфальте данная система поможет остановить машину быстрее, а вот в гололед она позволит сохранить управление, но дистанция торможения при этом станет длиннее;
трезвое состояние водителя. Адекватный водитель быстрее реагирует на быстро меняющуюся ситуацию на дороге, благодаря чему, он быстрее остановит свой транспорт при необходимости;
отсутствие отвлекающих факторов во время движения. Зачастую замедленная реакция автомобилиста связана с тем, что он отвлекается и не следит за дорогой. Самый распространенный фактор отвлечения внимания – это мобильный телефон. Из-за замедления реакции того, кто управляет авто, путь торможения увеличивается.
Онлайн калькулятор
Скорость передачи данных
Объём данных (размер файла) I = битбайткилобит (Kбит)кибибит (Кибит)килобайт (Кбайт)кибибайт (КиБ)мегабит (Мбит)мебибит (Мибит)мегабайт (Мбайт)мебибайт (МиБ)гигабит (Гбит)гибибит (Гибит)гигабайт (Гбайт)гибибайт (ГиБ)терабит (Тбит)тебибит (Тибит)терабайт (Тбайт)тебибайт (ТиБ)Время передачи данных t = секминчассуткигодСкорость передачи данных V =
бит в секунду (бит/с)байт в секунду (Б/с)килобит в секунду (Kбит/с)кибибит в секунду (Кибит/с)килобайт в секунду (Кбайт/с)кибибайт в секунду (КиБ/с)мегабит в секунду (Мбит/с)мебибит в секунду (Мибит/с)мегабайт в секунду (Мбайт/с)мебибайт в секунду (МиБ/с)гигабит в секунду (Гбит/с)гибибит в секунду (Гибит/с)гигабайт в секунду (Гбайт/с)гибибайт в секунду (ГиБ/с)терабит в секунду (Тбит/с)тебибит в секунду (Тибит/с)терабайт в секунду (Тбайт/с)тебибайт в секунду (ТиБ/с)Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*
Объём данных
Скорость передачи данных V = бит в секунду (бит/с)байт в секунду (Б/с)килобит в секунду (Kбит/с)кибибит в секунду (Кибит/с)килобайт в секунду (Кбайт/с)кибибайт в секунду (КиБ/с)мегабит в секунду (Мбит/с)мебибит в секунду (Мибит/с)мегабайт в секунду (Мбайт/с)мебибайт в секунду (МиБ/с)гигабит в секунду (Гбит/с)гибибит в секунду (Гибит/с)гигабайт в секунду (Гбайт/с)гибибайт в секунду (ГиБ/с)терабит в секунду (Тбит/с)тебибит в секунду (Тибит/с)терабайт в секунду (Тбайт/с)тебибайт в секунду (ТиБ/с)Время передачи данных t = секминчассуткигодОбъём данных (размер файла) I =
битбайткилобит (Kбит)кибибит (Кибит)килобайт (Кбайт)кибибайт (КиБ)мегабит (Мбит)мебибит (Мибит)мегабайт (Мбайт)мебибайт (МиБ)гигабит (Гбит)гибибит (Гибит)гигабайт (Гбайт)гибибайт (ГиБ)терабит (Тбит)тебибит (Тибит)терабайт (Тбайт)тебибайт (ТиБ)Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*
Время передачи данных
Объём данных (размер файла) I = битбайткилобит (Kбит)кибибит (Кибит)килобайт (Кбайт)кибибайт (КиБ)мегабит (Мбит)мебибит (Мибит)мегабайт (Мбайт)мебибайт (МиБ)гигабит (Гбит)гибибит (Гибит)гигабайт (Гбайт)гибибайт (ГиБ)терабит (Тбит)тебибит (Тибит)терабайт (Тбайт)тебибайт (ТиБ)Скорость передачи данных V = бит в секунду (бит/с)байт в секунду (Б/с)килобит в секунду (Kбит/с)кибибит в секунду (Кибит/с)килобайт в секунду (Кбайт/с)кибибайт в секунду (КиБ/с)мегабит в секунду (Мбит/с)мебибит в секунду (Мибит/с)мегабайт в секунду (Мбайт/с)мебибайт в секунду (МиБ/с)гигабит в секунду (Гбит/с)гибибит в секунду (Гибит/с)гигабайт в секунду (Гбайт/с)гибибайт в секунду (ГиБ/с)терабит в секунду (Тбит/с)тебибит в секунду (Тибит/с)терабайт в секунду (Тбайт/с)тебибайт в секунду (ТиБ/с)Время передачи данных t =
секминчассуткигодОкругление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*
Движение тела, брошенного вертикально вверх
Движение тела, брошенного вертикально вверх, описывается в два этапа
Если известна скорость в момент времени t, для определения перемещения используется следующая формула:
Если время движения неизвестно, для определения перемещения используется следующая формула:
Формула определения скорости:
Какой знак выбрать — «+» или «–» — вам помогут правила:
- Если движение равнозамедленное (тело поднимается вверх), перед ускорением свободного падения в формуле нужно ставить знак «–», так как векторы скорости и ускорения противоположно направлены.
- Если движение равноускоренное (тело падает вниз), перед ускорением свободного падения в формуле нужно ставить знак «+», так как векторы скорости и ускорения сонаправлены.
Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h2 > h1). По этой же причине время второго этапов движения тоже будет больше (t2 > t1). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (v2 > v01).
Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.
Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:
Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).
Таблица расстояний между городами
Подготовится к поезде, проложить автомаршрут и рассчитать расход топлива на поездку между городами используя расчёт расстояний может каждый из вас. Калькулятор расстояний поможет понять, как доехать до нужной области, города, населённого пункта или страны мира по автомобильным дорогам. Рассчитать расстояние и рассчитать стоимость поездки по маршруту, а также определить расход топлива на 1 километр пути теперь очень просто. Вам нужно знать направление поездки, расход топлива вашего автомобиля и знать сколько сегодня стоит бензин дизель или газ. Расчёт расстояний онлайн показывает расход топлива на грузовом или легковом автомобиле, который потребуется для поездки по выбранному маршруту. Вам больше не потребуется атлас автомобильных дорог потому, что дорожные карты находится в нашем онлайн сервисе, который позволяет рассчитать маршрут и расстояние по автодорогам. Также, вам не придётся использовать устаревший курвиметр, линейки и прочие таблицы расстояний между городами. Наша программа, это калькулятор расстоянии, который прокладывает точный маршрут и помогает определить расход топлива на вашем ТС по автомобильным дорогам России, СНГ, Европы и Азии.
Кто использует расчёт расстояний между городами?
Всем людям, которые хотят рассчитать расстояние между городами и проложить маршрут. Карта и расстояние, это то что должен знать любой водитель перед тем, как отправится в междугородний или международный реис на автомобиле;
Любой человек, который поехал путешествовать на авто
Не важно один или с семьей. Он должен заранее рассчитать расстояние между городами, чтобы знать сколько топлива и денег потребуется на поездку в нужный город, населённый пункт или страну на карте мира;
Водители грузовиков и дальнобойщики, ежедневно используют расчет расстояний между городами, чтобы проложить маршрут по карте автодорог и рассчитать затраты на топливо, зная сколько топлива расходует их грузовой автомобиль;
Грузоотправитель и получатель груза должны всегда использовать калькулятор расстояний или таблицу расстояний
Расстояние между городами, километраж, маршрут, цена и расход топлива формируют ценообразование в грузоперевозках;
Все транспортные компании в сфере грузоперевозок, сначала считают расстояние между городами км. Потом свои затраты и расход топлива на грузовом автомобиле, после чего озвучивают заказчику тарифы на перевозку груза;
Калькулятор расхода топлива и расчет расстояний между городами позволит вам сравнить тарифы транспортных компании для понимания процессов грузовой логистики. Вы должны знать, как формируются цены отрасли перевозок;
Менеджер логист, экспедитор, автодиспетчер и АТИ специалисты должны знать расстояние между городами. Ежедневно они используют расчёт расстояний между городами мира планируя маршрут перевозки груза для своих заказчиков;
Расчет расстояний информирует людей о факторах влияющих на удорожание перевозки грузов. Расчёт расстояний позволяет развиться компаниям грузовой отрасли за счёт грамотной консультации клиентов о сроках доставки и маршрутах перевозки.
Расчёт расстояний и расход топлива просто незаменим при учёте финансовой составляющей маршрута. Всегда нужно понимать количество потраченного топлива, его цену и расходы планируя маршрут движения на авто. Расстояния между населёнными пунктами мира складываются из дорожных участков автодорог на основе Яндекс карты и Гугл карты с корректировкой на спутниковые снимки.
Скорость не меняется
Пусть тело движется по прямой и при этом его скорость не изменяется (остается одной и той же). На языке математики «скорость не изменяется» можно записать так:
\
На графике для скорости v(t) такая скорость обозначается горизонтальной линией. На рисунке 2 эта линия обозначена синим цветом.
 Рис.2. Площадь прямоугольника на графике v(t), если скорость тела не изменяется, будет численно равна перемещению тела
Рис.2. Площадь прямоугольника на графике v(t), если скорость тела не изменяется, будет численно равна перемещению тела
Примечание: Движение с постоянной (т. е. с одной и той же) скоростью называют равномерным движением.
Если скорость направлена по оси движения – линия лежит выше оси t времени (рис. 2а).
А когда скорость направлена против оси движения – линия скорости располагается ниже оси t времени (рис. 2б). Математики в таком случае говорят: «Скорость имеет отрицательную проекцию на ось».
Какую бы проекцию не имела скорость – положительную, или отрицательную, длина вектора скорости остается положительной. Поэтому, когда мы вычисляем площадь фигуры, то не учитываем знак «минус» для скорости (рис. 2б).
В обоих случаях перемещение тела можно вычислить по формуле:
\
Примечание: Перемещение тела – это всегда либо нулевая, либо положительная величина S. Математики словосочетание «либо нулевая, либо положительная» заменят одним словом «не отрицательная».
Онлайн конвертер
бит в секунду (бит/с)байт в секунду (Б/с)килобит в секунду (Kбит/с)кибибит в секунду (Кибит/с)килобайт в секунду (Кбайт/с)кибибайт в секунду (КиБ/с)мегабит в секунду (Мбит/с)мебибит в секунду (Мибит/с)мегабайт в секунду (Мбайт/с)мебибайт в секунду (МиБ/с)гигабит в секунду (Гбит/с)гибибит в секунду (Гибит/с)гигабайт в секунду (Гбайт/с)гибибайт в секунду (ГиБ/с)терабит в секунду (Тбит/с)тебибит в секунду (Тибит/с)терабайт в секунду (Тбайт/с)тебибайт в секунду (ТиБ/с) =бит в секунду (бит/с)байт в секунду (Б/с)килобит в секунду (Kбит/с)кибибит в секунду (Кибит/с)килобайт в секунду (Кбайт/с)кибибайт в секунду (КиБ/с)мегабит в секунду (Мбит/с)мебибит в секунду (Мибит/с)мегабайт в секунду (Мбайт/с)мебибайт в секунду (МиБ/с)гигабит в секунду (Гбит/с)гибибит в секунду (Гибит/с)гигабайт в секунду (Гбайт/с)гибибайт в секунду (ГиБ/с)терабит в секунду (Тбит/с)тебибит в секунду (Тибит/с)терабайт в секунду (Тбайт/с)тебибайт в секунду (ТиБ/с)Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*
Чтобы перевести скорость передачи данных из одних единиц измерения в другие, введите значение и выберите единицы измерения скорости.
Задачи по кинематике, их решение
Задача 1
Рассмотрим путь велосипедиста из одного населенного пункта в другой. Половина расстояния была преодолена со скоростью 12 км/ч (\(v_1\)). Далее половину оставшегося времени он ехал со скоростью 6 км/ч (\(v_2\)). Остаток расстояния путник преодолел пешком со скоростью 4км/ч (\(v_3\)). Необходимо рассчитать среднюю скорость на всем пути следования велосипедиста.
Решение
Данный пример относится к теме равномерного прямолинейного движения одного тела. Процесс можно изобразить схематично:
\(S = S_1 + S_2 + S_3\)
\(t = t_1 + t_2 + t_3\)
На каждый отрезок пути необходимо составить уравнение движения:
\(S_1 = v_1t_1\)
\(S_2 = v_2t_2\)
\(S_3 = v_3t_3\)
Далее можно представить дополнительные условия задачи:
\(S_1 = S_2 + S_3\)
\(t_2 = t_3\)
\(v_{sr}=\frac{S}{t}=\frac{S_{1}+S_{2}+S_{3}}{t_{1}+t_{2}+t_{3}}\)
Следует преобразить формулу и подставить числовые значения:
\(v_{sr}=\frac{2S_{1}}{\frac{S_{1}}{v_{1}}+\frac{2S_{1}}{v_{2}+v_{3}}}=\frac{2v_{1}\left(v_{2}+v_{3} \right)}{2v_{1}+v_{2}+v_{3}}\)
\(v_{sr}=\frac{2\times 12\left(6+4 \right)}{2\times 12+6+4}=7\)
Ответ: средняя скорость составляет \(7\) км/ч.
Задача 2
Тело подбросили вертикально вверх. Начальная скорость при этом составила 3,13 м/с (\(v_0\)). В момент, когда данное тело достигло максимальную высоту полета, из начального пункта подбросили второе тело с такой же начальной скоростью, как у первого. Необходимо определить на каком расстоянии от точки бросания встретятся тела. Сопротивлением воздуха при решении можно не учитывать.
Решение
Схематично перемещение тел можно представить следующим образом:
Формула, описывающая движение тела, которое подбросили вверх, необходима для вычисления координаты движущегося тела в любое время. Для первого тела справедливо уравнение:
\(h=v_{0}t_{1}-\frac{gt_{1}^{2}}{2}\)
Для второго тела можно представить следующую формулу:
\(h=v_{0}t_{2}-\frac{gt_{2}^{2}}{2}\)
Следующую формулу можно составить на основании условия задачи, в котором указано, что второе тело бросили позднее первого на время максимального подъема:
\(t_{1}-t_{2}=\frac{v_{0}}{g}\)
Объединяя уравнения в систему из трех формул относительно величины \(h\) получим:
\(h=\frac{3}{4}\frac{v_{0}^{2}}{2g}\)
\(h=\frac{3}{4}\frac{3.13^{2}}{2*9.8}=0.37\)
Ответ: тела встретятся на высоте \(0,37\) м.
Задача 3
Камень, находясь в свободном падении, вторую часть пути преодолел за 1 секунду. Необходимо вычислить высоту \(h\), с которой упал камень.
Решение
Ось Y системы координат, в которых падает камень, направлена вертикально вниз. В качестве начала координат можно принять точку, из которой камень упал. Закон перемещения данного тела в проекции на ось будет обладать следующим видом:
\(h=v_{0}t+\frac{gt^{2}}{2}\)
\(h=\frac{gt^{2}}{2}\)
\(v=v_{0}t+gt\)
\(v=gt\)
Время падения камня рассчитывается по формуле:
\(t=\sqrt{\frac{2h}{g}}\)
Для середины пути, который преодолел камень, справедливы уравнения:
\(\frac{h}{2}=\frac{gt_{1}^{2}}{2}\)
\(t_{1}=\sqrt{\frac{h}{g}}\)
Время \(t_2\), которое потребовалось телу на преодоление второй половины пути, указанное в условии задачи, рассчитывается по формуле:
\(t_{2}=t-t_{1}=\sqrt{\frac{2h}{g}}-\sqrt{\frac{h}{g}}\)
\(t_{2}^{2}=\frac{h}{g}\left(\sqrt{2} -1\right)^{2}\)
Исходя из данного уравнения, можно вычислить высоту:
\(t_{2}^{2}=\frac{h}{g}\left(\sqrt{2} -1\right)^{2}\)
\(h=\frac{t_{2}^{2}g}{\left(\sqrt{2}-1 \right)^{2}}=\frac{9,81}{0,17}=57,7\)
Ответ: камень упал с высоты \(57,7\) м.
Как найти скорость, если известно время и расстояние?
Для то, чтобы найти скорость, если известно время и расстояние, нужно расстояние разделить на время. Пример такой задачи:
Решение задачи на движение:
- В черновик записываем, что нам известно расстояние и время.
- Из условия задачи определяем, что нужно найти скорость
- Вспоминаем формулу для нахождения скорости.
Формулы для решения таких задач показаны на картинке ниже.
Формулы для решения задач про расстояние, время и скорость
Подставляем известные данные и решаем задачу:
Расстояние до норы — 3 километра
Время, за которое Заяц добежал до норы — 3 минуты
Скорость — неизвестна
Запишем эти известные данные математическими знаками
S — 3 километра
t — 3 минуты
v — ?
Записываем формулу для нахождения скорости
v = S : t
Теперь запишем решение задачи цифрами:
v = 3 : 3 = 1 км/мин
Волк может бежать со скоростью 60 км/час
Теория относительности Альберта Эйнштейна
В свое время Альберт Эйнштейн явил миру теорию относительности, о которой вы наверняка слышали. Она полностью меняет типичное представление о времени и взгляд на него. Согласно этой теории, прогрессия времени не универсальна. Если говорить совсем просто, то по этой теории часы идут с разной скоростью в зависимости от того, на чьей руке они надеты.
Если обладатель часов окажется в непривычной для него ситуации, например, будет перемещаться со скоростью света или окажется рядом с сильным источником гравитационных волн — например, рядом с черной дырой — время для него пойдет иначе. В некоторых ситуациях оно может даже остановиться или и вовсе повернутся вспять.
Проще говоря, в такой ситуации восприятие привычных физических процессов меняется и человек оказавшийся в таком месте может не только наблюдать время, но и двигаться по нему как в обычном пространстве — влево, вправо, вперед, назад и так далее. То есть, относительность уравнивает время и пространство, наделяя их одними и теми же свойствами.

Величайшие умы мира бьются над разгадкой тайны времени, но они ничего пока так и не добились.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло
А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости
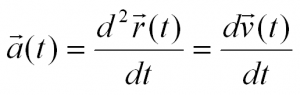
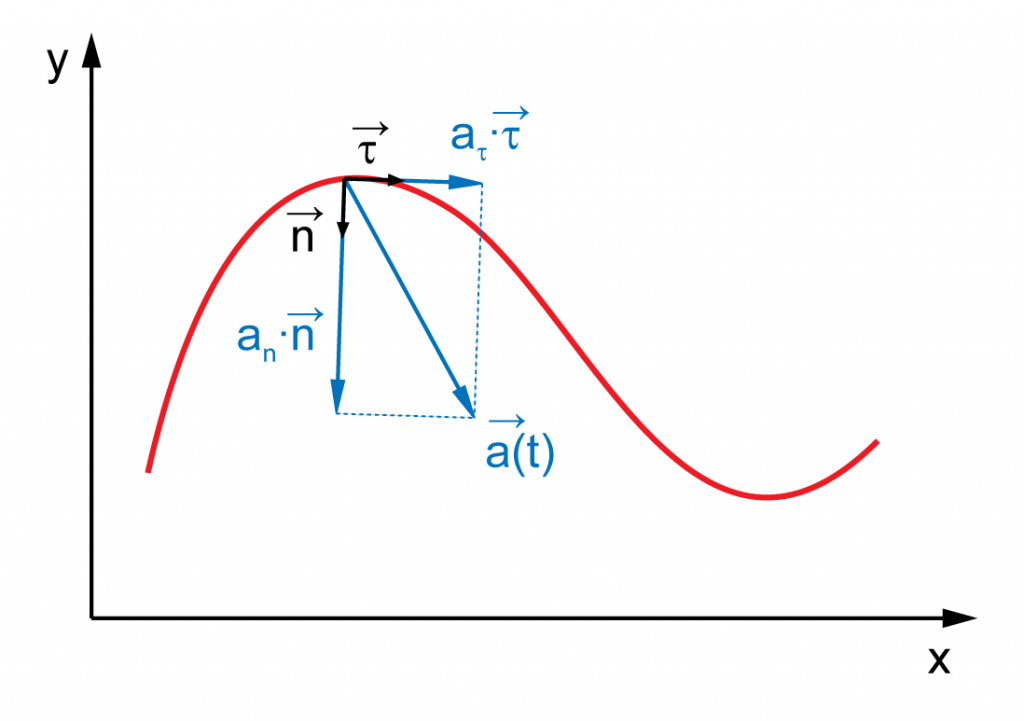
Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории
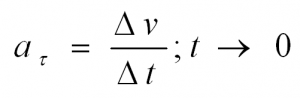
Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.
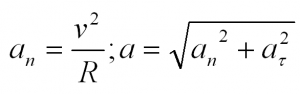
Здесь R – радиус окружности, по которой движется тело.
Средняя скорость
Факт изменения скорости тела при неравномерном движении не всегда необходимо учитывать, при рассмотрении движении тела на большом участке пути в целом (нам не важна скорость в каждый момент времени) удобно ввести понятие средней скорости.
Например, делегация школьников добирается из Новосибирска в Сочи поездом. Расстояние между этими городами по железной дороге составляет приблизительно 3300 км. Скорость поезда, когда он только выехал из Новосибирска составляла
Рис. 6. Иллюстрация к примеру
Когда рассматривается движение тела на большом участке пути в целом, удобнее ввести понятие средней скорости.
Средней скоростью называют отношение полного перемещения, которое совершило тело, ко времени, за которое совершено это перемещение (рис. 7).
Рис. 7. Средняя скорость
Данное определение не всегда является удобным. Например, спортсмен пробегает 400 м – ровно один круг. Перемещение спортсмена равно 0 (рис. 8), однако мы понимаем, что его средняя скорость нулю равна быть не может.
Рис. 8. Перемещение равно 0
На практике чаще всего используется понятие средней путевой скорости.
Средняя путевая скорость – это отношение полного пути, пройденного телом, ко времени, за которое путь пройден (рис. 9).
Рис. 9. Средняя путевая скорость
Существует еще одно определение средней скорости.
Средняя скорость – это та скорость, с которой должно двигаться тело равномерно, чтобы пройти данное расстояние за то же время, за которое оно его прошло, двигаясь неравномерно.
Из курса математики нам известно, что такое среднее арифметическое. Для чисел 10 и 36 оно будет равно:
Для того чтобы узнать возможность использования этой формулы для нахождения средней скорости, решим следующую задачу.
Велосипедист поднимается со скоростью 10 км/ч на склон, затрачивая на это 0,5 часа. Далее со скоростью 36 км/ч спускается вниз за 10 минут. Найдите среднюю скорость велосипедиста (рис. 10).
Рис. 10. Иллюстрация к задаче
Дано:Найти:
Так как единица измерения данных скоростей – км/ч, то и среднюю скорость найдем в км/ч. Следовательно, данные задачи не будем переводить в СИ. Переведем
Средняя скорость равна:
Полный путь (
Путь подъема на склон равен:
Путь спуска со склона равен:
Время, за которое пройден полный путь, равно:
Ответ:
Исходя из ответа задачи, видим, что применять формулу среднего арифметического для вычисления средней скорости нельзя.
Не всегда понятие средней скорости полезно для решения главной задачи механики. Возвращаясь к задаче про поезд, нельзя утверждать, что если средняя скорость на всем пути поезда равна Мгновенная скорость
Среднюю скорость, измеренную за бесконечно малый промежуток времени, называют мгновенной скоростью тела (для примера: спидометр автомобиля (рис. 11) показывает мгновенную скорость).
Рис. 11. Спидометр автомобиля показывает мгновенную скорость
Существует еще одно определение мгновенной скорости.
Мгновенная скорость – скорость движения тела в данный момент времени, скорость тела в данной точке траектории (рис. 12).
Рис. 12. Мгновенная скорость
Для того чтобы лучше понять данное определение, рассмотрим пример.
Пусть автомобиль движется прямолинейно по участку шоссе. У нас есть график зависимости проекции перемещения от времени для данного движения (рис. 13), проанализируем данный график.
Рис. 13. График зависимости проекции перемещения от времени
На графике видно, что скорость автомобиля не постоянная. Допустим, необходимо найти мгновенную скорость автомобиля через 30 секунд после начала наблюдения (в точке A). Пользуясь определением мгновенной скорости, найдем модуль средней скорости за промежуток времени от
Рис. 14. График зависимости проекции перемещения от времени
Рассчитываем среднюю скорость на данном участке времени:
Для того чтобы проверить правильность нахождения мгновенной скорости, найдем модуль средней скорости за промежуток времени от
Рис. 15. График зависимости проекции перемещения от времени
Рассчитываем среднюю скорость на данном участке времени:
Получили два значения мгновенной скорости автомобиля через 30 секунд после начала наблюдения. Точнее будет то значение, где интервал времени меньше, то есть
A
Мгновенная скорость – это векторная величина. Поэтому, кроме ее нахождения (нахождения ее модуля), необходимо знать, как она направлена.
Направление мгновенной скорости совпадает с направлением перемещения тела.
Если тело движется криволинейно, то мгновенная скорость направлена по касательной к траектории в данной точке (рис. 16).
Рис. 16. Направление мгновенной скорости
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Как рассчитать полное время остановки и итоговый тормозной путь?
Итак, итоговое значение этого пути включает в себя не только расстояние торможения, но и дистанцию реакции автомобилиста.
Чтобы рассчитать расстояние, которое пройдет авто за время реакции водителя, необходимо воспользоваться следующей формулой:
Sреакции = V / 10 * 3, где
V – это скорость транспортного средства.
Таким образом, итоговый тормозной путь будет равняться сумме двух значений: пути реакции автомобилиста и пути торможения:
Sитог = Sторм + Sреакции
Возвращаясь к примеру, в котором машина движется летом по сухому асфальту со скоростью 80 км/ч, рассчитаем дистанцию реакции.
Sреакции = 80/10 * 3 = 24 метра
Теперь, когда мы знаем, что дистанция торможения равна 36 метрам, а расстояние реакции – 24 метра, можно рассчитать его итоговое значение:
Sитог = 36 + 24 = 60 метров
Соответственно, полное время остановки – это временной период, за который машина пройдет итоговый тормозной путь. Это время складывается из времени реакции водители и времени, затраченного на тормозную дистанцию.
Формула его расчета следующая:
, где:
– время реакции водителя;
– время срабатывания тормозного привода;
– время нарастания тормозных сил;
– начальная скорость торможения;
– ускорение свободного падения;
– коэффициент продольного сцепления с дорогой колёс автомобиля;
– коэффициент эффективности торможения.
Итак, итоговое остановочное расстояние включает в себя дистанцию реакции водителя и тормозной путь. На каждую из этих величин влияют определенные факторы. Чтобы сократить значение итоговой величины, необходимо соблюдать скоростной режим, следить за исправностью автомобиля, учитывать его загруженность и садиться за руль исключительно в адекватном состоянии.

Эта тема закрыта для публикации ответов.





