Формула расчета расстояния по координатам
Пусть и являются географическими широтой и долготой двух точек 1 и 2, и — их абсолютная разность. Тогда , центральный угол между ними, определяется теоремой сферических косинусов:
Формула расстояние d т.е.длины дуги, для сферы радиуса R и приведены в радианах
Больше матиматики …
На компьютерных системах с низкой точностью с плавающей запятой, эта формула может иметь большие ошибки округления, если расстояние не большое (если две точки находятся в 1 км друг от друга на поверхности Земли, косинус центрального угла выходит 0,99999999). Для современных 64-разрядных чисел с плавающей запятой, формула Теоремы косинусов, которая приведенна выше, не имеет серьезных ошибок округления для расстояний более нескольких метров на поверхности Земли. Эта формула лучше подходит для вычисления растояние по координатам на небольшые расстояния
Для получения более точных рузультатов на большых расстояниях стараются исполтзовать формулу посложнее, в которой сделано предположение, что сфера является эллипсоидом с одинаковыми большой и малой осями.
Более подробную информацию о выведении формулы расчета расстояния по координатам читайте здесь: http://en.wikipedia.org/wiki/Great_circle_distance
Комментарии:
Обработка «Распознавание штрихкода с помощью утилиты Zbar» для Документооборот ред. 2 Промо
В связи с тем, что стандартный функционал программы «Документооборот» ред. 2.1 дает возможность распознавания штрихкодов только форма EAN-13, данная обработка — альтернативный способ для распознавания штрихкода в программе 1С: Документооборот ред. 2 с помощью утилиты Zbar, которая распознает в том числе и в формате Code 128 (один из стандартных штрихкодов кодирования документов, например, «Управление торговлей» ред. 11), а также с возможностью поэтапно проследить все действия от распознавания до прикрепления к документу или простой загрузки в каталоги файлов в базе 1С.
5 стартмани
Навигатор по конфигурации базы 1С 8.3 Промо
Универсальная внешняя обработка для просмотра метаданных конфигураций баз 1С 8.3.
Отображает свойства и реквизиты объектов конфигурации, их количество, основные права доступа и т.д.
Отображаемые характеристики объектов: свойства, реквизиты, стандартные рекизиты, реквизиты табличных частей, предопределенные данные, регистраторы для регистров, движения для документов, команды, чужие команды, подписки на события, подсистемы.
Отображает структуру хранения объектов базы данных, для регистров доступен сервис «Управление итогами».
Платформа 8.3, управляемые формы. Версия 1.1.0.85 от 10.10.2021
3 стартмани
Другая формула
Можно создать другое выражение, чтобы найти кратчайшее расстояние от точки до линии. Этот вывод также требует, чтобы линия не была вертикальной или горизонтальной.
Точка P задана координатами ( ). Уравнение линии задается формулой . Уравнение нормали этой линии , которая проходит через точку Р дается .
Икс,у{\ displaystyle x_ {0}, y_ {0}}узнак равномИкс+k{\ displaystyle y = mx + k}узнак равноИкс-Иксм+у{\ displaystyle y = {\ frac {x_ {0} -x} {m}} + y_ {0}}
Точка, в которой эти две прямые пересекаются, является ближайшей точкой на исходной прямой к точке P. Следовательно:
- мИкс+kзнак равноИкс-Иксм+у.{\ displaystyle mx + k = {\ frac {x_ {0} -x} {m}} + y_ {0}.}
Мы можем решить это уравнение относительно x ,
- Иксзнак равноИкс+му-мkм2+1.{\ displaystyle x = {\ frac {x_ {0} + my_ {0} -mk} {m ^ {2} +1}}.}.
У координаты точки пересечения можно найти, подставив это значение х в уравнение исходной линии,
- узнак равном(Икс+му-мk)м2+1+k.{\ displaystyle y = m {\ frac {(x_ {0} + my_ {0} -mk)} {m ^ {2} +1}} + k.}
Используя уравнение для нахождения расстояния между двумя точками, мы можем сделать вывод, что формула для нахождения кратчайшего расстояния между линией и точкой следующая:
dзнак равно(Икс2-Икс1)2+(Y2-Y1)2{\ displaystyle d = {\ sqrt {(X_ {2} -X_ {1}) ^ {2} + (Y_ {2} -Y_ {1}) ^ {2}}}}
- dзнак равно(Икс+му-мkм2+1-Икс)2+(мИкс+му-мkм2+1+k-у)2знак равно|k+мИкс-у|1+м2.{\ displaystyle d = {\ sqrt {\ left ({{\ frac {x_ {0} + my_ {0} -mk} {m ^ {2} +1}} — x_ {0}} \ right) ^ { 2} + \ left ({m {\ frac {x_ {0} + my_ {0} -mk} {m ^ {2} +1}} + k-y_ {0}} \ right) ^ {2}} } = {\ frac {| k + mx_ {0} -y_ {0} |} {\ sqrt {1 + m ^ {2}}}}.}.}
Вспоминая, что m = — a / b и k = — c / b для прямой с уравнением ax + by + c = 0, небольшое алгебраическое упрощение сводит это к стандартному выражению.
Деление отрезка в заданном отношении
Мы уже научились находить коор-ты середины отрезка. Можно сказать, что середина – это точка, которая разбивает отрезок в отношении 1:1, то есть на равные отрезки. А что делать в более сложном случае, если нужно найти точку, разбивающую отрезок в другом отношении, например, в отношении 2:1? Выведем для такого случая формулу.
Пусть точка С разбивает отрезок АВ в некотором отношении так, что отрезок АС в k больше отрезка СВ:
(Примечание. Если отрезок АС меньше СВ, то число k будет меньше единицы.)
Как и обычно, для обозначения коор-т точек используем индексы, совпадающие с обозначением точек: А(xА; уА), В(xВ; уВ) и С(xС; уС).
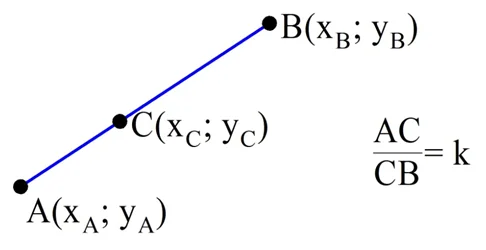
Нам также потребуются вектора АС{xАС; уАС} и СВ{xСВ; уСВ}. Так как эти вектора сонаправлены, и АС в k раз длиннее, то

Абсолютно аналогичные образования приведут к такому же выражению для коор-ты у:

Рассмотрим на примерах использование этой формулы.
Задание. На отрезке РM отложена точка K так, что она разбивает РM на отрезки РK и KM в отношении РK:KM = 2:1. Даны коор-ты точек: Р(6; 3) и К (18; 12). Вычислите коор-ты K.
Решение.
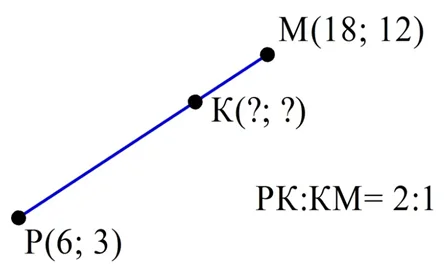
Отношение РК:КМ = 2:1 означает, что отрезок РК в 2 раза длиннее, чем КМ. Это означает, что в формуле

Задание. Точки B (5; – 16) и H(29; 24) соединены отрезком. Точка M на отрезке ВН отмечена так, что ВМ:МН = 3:5. Определите коор-ты точки М.
Решение. Из отношения ВМ:МН = 3:5 вытекает, что ВМ длиннее МН в
3/5 = 0,6 раз
то есть фактически ВМ короче МН. То есть при использовании формулы

Рассмотрим ещё несколько более усложненных задач с использованием коор-т.
Задание. Точка K лежит на оси Ох, при этом она равноудалена от точек Е(2; 2) и F(6; 10). Найдите коор-ты К.
Решение. У любой точки, лежащей на оси Ох, коор-та у будет равна нулю, в том числе и у точки К:
yk = 0
Будем обозначать неизвестную коор-ту К как х:
xk = x
Напомним расстояние между точками можно рассчитать, используя формулу:

Получили иррациональное уравнение. В данном случае можно просто приравнять подкоренные выражения, однако после получения корней надо проверить, нет ли среди них посторонних:
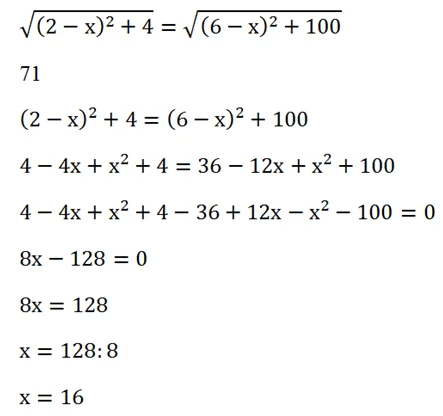
Проверяем, не является ли корень посторонним. Для этого просто подставляем его в уравнение:
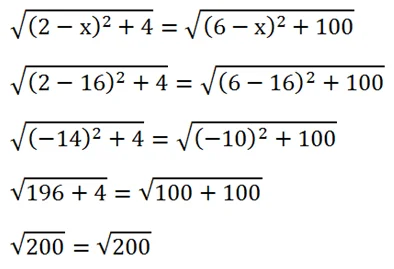
Корень действительно подошел, поэтому коор-та х точки К равна 16.
Ответ: (16; 0).
Моя реализация на РНР
// Радиус земли
define('EARTH_RADIUS', 6372795);
/*
* Расстояние между двумя точками
* $φA, $λA - широта, долгота 1-й точки,
* $φB, $λB - широта, долгота 2-й точки
* Написано по мотивам http://gis-lab.info/qa/great-circles.html
* Михаил Кобзарев <mikhail@kobzarev.com>
*
*/
function calculateTheDistance ($φA, $λA, $φB, $λB) {
// перевести координаты в радианы
$lat1 = $φA * M_PI / 180;
$lat2 = $φB * M_PI / 180;
$long1 = $λA * M_PI / 180;
$long2 = $λB * M_PI / 180;
// косинусы и синусы широт и разницы долгот
$cl1 = cos($lat1);
$cl2 = cos($lat2);
$sl1 = sin($lat1);
$sl2 = sin($lat2);
$delta = $long2 - $long1;
$cdelta = cos($delta);
$sdelta = sin($delta);
// вычисления длины большого круга
$y = sqrt(pow($cl2 * $sdelta, 2) + pow($cl1 * $sl2 - $sl1 * $cl2 * $cdelta, 2));
$x = $sl1 * $sl2 + $cl1 * $cl2 * $cdelta;
//
$ad = atan2($y, $x);
$dist = $ad * EARTH_RADIUS;
return $dist;
}
Пример вызова функции:
$lat1 = 77.1539; $long1 = -139.398; $lat2 = -77.1804; $long2 = -139.55; echo calculateTheDistance($lat1, $long1, $lat2, $long2) . " метров"; // Вернет "17166029 метров"
Точка и прямая
Прежде чем говорить, как найти расстояние от прямой до точки, необходимо подробно рассмотреть, о каких элементах идет речь.
Известно, что в двумерном или трехмерном пространстве в геометрии для определения места расположения того или иного объекта вводится специальная система координат. Удобнее всего использовать прямоугольную декартову систему, которая представляет собой пересекающиеся под прямым углом оси (2 для плоскости и 3 для трехмерного пространства). На каждой из них существует шкала в выбранных единицах.
Точечный объект
Или просто точка. Это нульмерный объект, который в двумерном пространстве представляет собой набор двух координат, а в трехмерном — трех. Математически точка записывается так: A (x1; y1), где x1 — ее координата по оси x, y1 — по оси y. Для определения значения координат необходимо от точки провести перпендикуляр к соответствующей оси, их пересечение укажет на искомое значение. Примеры разных точек на плоскости и пространстве:
- P (1; 0);
- Q (2; 3; -1);
- M (0; 0);
- N (-2; -1; 3).

Точка P лежит на оси x, а M в начале координатной системы. Обе они заданы на плоскости, в отличие от Q и N, которые можно построить в пространстве. Также следует отметить, что у координатных осей имеется положительное и отрицательное направления, поэтому точки могут иметь отрицательные координаты.
Уравнения линии
Прямая линия является одним из самых распространенных объектов в геометрии. С помощью нее строятся многие симметричные фигуры, например, пирамида, призма, треугольник, прямоугольник (но не сфера). Прямая линия представляет собой бесконечный объект в одном направлении, и нульмерный в двух других, если речь идет об объемном пространстве.
Для выполнения математических операций с геометрическим элементом существуют разные виды уравнений, которые его задают. Среди них можно назвать:
- общего типа;
- векторное;
- параметрическое;
- в отрезках.
Чаще всего в задачах применяют первые 2 вида. Универсальным уравнением, которое можно с легкостью преобразовать в любые другие формы, является векторное. Задается для трехмерного случая оно следующим образом:
(x; y; z) = (x0; y0; z0) + α*(vx; vy; vz).

Здесь (x; y; z) — координаты произвольной точки, которая принадлежит заданной прямой, (x0; y0; z0) — известная точка, лежащая на объекте, v (vx; vy; vz) — вектор, параллельно которому проходит прямая, он называется направляющим, α — произвольный числовой параметр, который может иметь положительные или отрицательные значения. Очевидно, что для плоского случая количество координат для каждого элемента будет равно двум.
Векторным уравнением удобно пользоваться, поскольку его легко преобразовать в параметрическое или в отрезках. В первом случае получается следующая система:
- x = x0 + α*vx;
- y = y0 + α*vy;
- z = z0 + α*vz.
Для уравнения в отрезках получается такое равенство:
(x-x0)/vx = (y-y0)/vy = (z-z0)/vz.
Чтобы получить из векторной формы уравнение общего типа для случая на плоскости, достаточно написать выражение в отрезках, а затем из него выразить y через x. В итоге получается такой вид:
y = vy/vx*(x — x0) + y0.
Расстояние между двумя точками на координатной прямой.
Давайте для начала определимся с обозначениями. Расстояние от точки А до точки В будем обозначать как .
Пусть задана координатная прямая Ox (точка О – начало отсчета) и некоторая точка А на ней. Мы знаем, что каждой точке на координатной прямой соответствует единственное действительное число. Пусть точке А соответствует действительное число , то есть, точка А имеет координату .
Как же определяется расстояние от начала отсчета до точки А? Вообще, измерение расстояния основано на сравнении отрезков — отрезка, соответствующего измеряемому расстоянию от точки до точки, и отрезка, принятого за единицу измерения.
Для точки А, которой соответствует целое число, все очень просто. Мы от точки О вдоль прямой OA последовательно откладываем единичные отрезки, пока не попадем в точку А. Количество единичных отрезков и дает нам расстояние между точками О и А.
Это достаточно очевидно. К примеру, чтобы попасть в точку А, которой соответствует число 2, нам нужно преодолеть расстояние в две единицы от начала отсчета в положительном направлении. Если точка А имеет координату -5, то нам придется отложить один за другим пять единичных отрезков в отрицательном направлении. То есть, в первом случае расстояние равно двум, а во втором случае расстояние от точки О до точки А равно пяти.
Если точке А соответствует рациональное число, то мы можем попасть из начала координат в точку А при помощи последовательного откладывания некоторого количества целых единичных отрезков и его части.
К примеру, если точка А имеет координату , то нам придется отложить один целый единичный отрезок в отрицательном направлении и еще половину от единичного отрезка. В этом случае расстояние равно . Следует отметить, что геометрическими построениями далеко не всегда можно разбить единичный отрезок на необходимое количество частей (например, попробуйте получить единичного отрезка).
Еще интереснее обстоит дело с определением расстояния от точки О до точки А, которой соответствует иррациональное число. К примеру, пусть точке А соответствует число . С помощью откладывания единичного отрезка и его частей от начала отсчета попасть в эту точку не так то просто. В этом случае прибегаем к абстракции: если координата точки А является положительным числом (), то это число принимаем в качестве расстояния, то есть , если же координата точки А есть отрицательное число (), то .
Очевидно, что последнее утверждение справедливо для любого действительного числа .
Итак, расстояние от начала отсчета до точки А, которой соответствует действительное число на координатной прямой, равно
- , если точка А совпадает с началом координат;
- , если ;
- , если .
С помощью знака модуля расстояние от точки О до точки А с координатой можно записать как (смотрите статью модуль числа).
Отсюда можно заключить, что расстояние от точки А с координатой до точки В с координатой равно модулю разности координат, то есть, при любом расположении точек на координатной прямой.
Расстояние от точки до прямой – определение.
Расстояние от точки до прямой определяется через расстояние от точки до точки. Покажем как это делается.
Пусть на плоскости или в трехмерном пространстве задана прямая a и точка M1, не лежащая на прямой a. Проведем через точку M1 прямую b, перпендикулярную прямой a. Обозначим точку пересечения прямых a и b как H1. Отрезок M1H1 называется перпендикуляром, проведенным из точки M1 к прямой a.
Определение.
Расстоянием от точки M1 до прямой a называют расстояние между точками M1 и H1.
Однако чаще встречается определение расстояния от точки до прямой, в котором фигурирует длина перпендикуляра.
Определение.
Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой.
Это определение эквивалентно первому определению расстояния от точки до прямой.
Обратите внимание на то, что расстояние от точки до прямой – это наименьшее из расстояний от этой точки до точек заданной прямой. Покажем это.. Возьмем на прямой a точку Q, не совпадающую с точкой M1
Отрезок M1Q называют наклонной, проведенной из точки M1 к прямой a. Нам нужно показать, что перпендикуляр, проведенный из точки M1 к прямой a, меньше любой наклонной, проведенной из точки M1 к прямой a. Это действительно так: треугольник M1QH1 прямоугольный с гипотенузой M1Q, а длина гипотенузы всегда больше длины любого из катетов, следовательно, .
Возьмем на прямой a точку Q, не совпадающую с точкой M1. Отрезок M1Q называют наклонной, проведенной из точки M1 к прямой a. Нам нужно показать, что перпендикуляр, проведенный из точки M1 к прямой a, меньше любой наклонной, проведенной из точки M1 к прямой a. Это действительно так: треугольник M1QH1 прямоугольный с гипотенузой M1Q, а длина гипотенузы всегда больше длины любого из катетов, следовательно, .
Групповая обработка прикрепленных файлов
Кому не знакомы авралы в бухгалтерии, когда налоговая требует представить копии всех документов за два-три года? Кто не получал сюрпризов в виде отсутствия документов, когда завтра их нужно уже представлять проверяющим? 1С предлагает прикрепление и хранение копий документов (в том числе со сканера) в базе, а данная обработка решает вопрос их быстрой подборки, сортировки и выгрузки, а также быстрого и эффективного контроля наличия или отсутствия документов в базе с формированием реестров как выгруженных, так и отсутствующих документов.
В настоящий момент обработка бесплатна, в дальнейшем планируется платная версия с расширенными возможностями.
Скажите решительное «Нет» авралам в бухгалтерии и штрафам за несвоевременное представление документов!
4 стартмани
Примеры решения задач на нахождение расстояния между точками
Пример 1
Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A(1-2) и B(11+2) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B.
Решение
- Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно OA=1-2=2-1
- Расстояние между точками A и B определим как модуль разности координат этих точек: AB=11+2-(1-2)=10+22
Ответ: OA=2-1, AB=10+22
Пример 2
Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A(1, -1) и B (λ+1, 3) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние АВ будет равно 5.
Решение
Чтобы найти расстояние между точками A и B, необходимо использовать формулу AB=(xB-xA)2+yB-yA2
Подставив реальные значения координат, получим:AB=(λ+1-1)2+(3-(-1))2=λ2+16
А также используем имеющееся условие, что АВ=5 и тогда будет верным равенство:
λ2+16=5λ2+16=25λ=±3
Ответ: АВ = 5, если λ=±3 .
Пример 3
Исходные данные: задано трехмерное пространство в прямоугольной системе координат Oxyz и лежащие в нем точки A (1, 2, 3) и B-7, -2, 4 .
Решение
Для решения задачи используем формулу AB=xB-xA2+yB-yA2+(zB-zA)2
Подставив реальные значения, получим: AB=(-7-1)2+(-2-2)2+(4-3)2=81=9
Ответ: |АВ| = 9
Всё ещё сложно?
Наши эксперты помогут разобраться
Все услуги
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве
Пример 5
Найти расстояние от точки с координатами M12, -4, -1 к прямой x+12=y-1=z+55.
Решение
Первый способ начинается с записи уравнения плоскости χ, проходящей через М1и перпендикулярно заданной точке. Получаем выражение вида:
2·(x-2)-1·(y-(-4))+5·(z-(-1))=⇔2x-y+5z-3=
Нужно найти координаты точки H1, являющейся точкой пересечения с плоскостью χ к заданной по условию прямой. Следует переходить от канонического вида к пересекающемуся. Тогда получаем систему уравнений вида:
x+12=y-1=z+55⇔-1·(x+1)=2·y5·(x+1)=2·(z+5)5·y=-1·(z+5)⇔x+2y+1=5x-2z-5=5y+z+5=⇔x+2y+1=5x-2z-5=
Необходимо вычислить систему x+2y+1=5x-2z-5=2x-y+5z-3=⇔x+2y=-15x-2z=52x-y+5z=3 по методу Крамера, тогда получаем, что:
∆=125-22-15=-60∆x=-125-23-15=-60⇔x=∆x∆=-60-60=1∆y=1-1552235=60⇒y=∆y∆=60-60=-1∆z=12-1552-13=⇒z=∆z∆=-60=
Отсюда имеем, что H1(1, -1, ).
Необходимо рассчитать расстояние между точками с координатами M1(2, -4, -1) и H1(1, -1, ) по формуле:
M1H1=1-22+-1—42+—12=11
Второй способ необходимо начать с поиска координат в каноническом уравнении
Для этого необходимо обратит внимание на знаменатели дроби. Тогда a→=2, -1, 5 является направляющим вектором прямой x+12=y-1=z+55
Необходимо вычислить длину по формуле a→=22+(-1)2+52=30.
Понятно, что прямая x+12=y-1=z+55 пересекает точку M3(-1, , -5), отсюда имеем, что вектор с началом координат M3(-1, , -5) и его концом в точке M12, -4, -1 является M3M1→=3, -4, 4. Находим векторное произведение a→=(2, -1, 5) и M3M1→=(3, -4, 4).
Мы получаем выражение вида a→×M3M1→=i→j→k→2-153-44=-4·i→+15·j→-8·k→+20·i→-8·j→=16·i→+7·j→-5·k→
получаем, что длина векторного произведения равняется a→×M3M1→=162+72+-52=330.
Имеются все данные для использования формулы вычисления расстояния от точки для прямлой, поэтому применим ее и получим:
M1H1=a→×M3M1→a→=33030=11
Ответ: 11.
Всё ещё сложно?
Наши эксперты помогут разобраться
Все услуги
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Расстояние между двумя параллельными прямыми: определение
Определение 1
Расстояние между двумя параллельными прямыми – это расстояние от некоторой произвольной точки одной из параллельных прямых до другой прямой.
Приведем иллюстрацию для наглядности:
На чертеже изображены две параллельные прямые a и b. Точка М1 принадлежит прямой a, из нее опущен перпендикуляр на прямуюb. Полученный отрезок М1Н1 и есть расстояние между двумя параллельными прямыми aиb.
Указанное определение расстояния между двумя параллельными прямыми справедливо как на плоскости, так и для прямых в трехмерном пространстве. Кроме того, данное определение взаимосвязано со следующей теоремой.
Теорема
Когда две прямые параллельны, все точки одной из них равноудалены от другой прямой.
Доказательство
Пусть нам заданы две параллельные прямые a и b. Зададим на прямой а точки М1 и М2, опустим из них перпендикуляры на прямую b, обозначив их основания соответственно как Н1 и Н2. М1Н1 – это расстояние между двумя параллельными прямыми по определению, и нам необходимо доказать, что |М1Н1|=|М2Н2|.
Пусть будет также существовать некоторая секущая, которая пересекает две заданные параллельные прямые. Условие параллельности прямых, рассмотренное в соответствующей статье, дает нам право утверждать, что в данном случае внутренние накрест лежащие углы, образованные при пересечении секущей заданных прямых, являются равными: ∠M2M1H2=∠H1H2M1. Прямая М2Н2 перпендикулярна прямой b по построению, и, конечно, перпендикулярна прямой a. Получившиеся треугольники М1Н1Н2 и М2М1Н2 являются прямоугольными и равными друг другу по гипотенузе и острому углу: М1Н2 – общая гипотенуза, ∠M2M1H2=∠H1H2M1. Опираясь на равенство треугольников, мы можем говорить о равенстве их сторон, т.е.: |М1Н1| = |М2Н2|. Теорема доказана.
Отметим, что расстояние между двумя параллельными прямыми – наименьшее из расстояний от точек одной прямой до точек другой.
Расчет расстояния между координатами
Данный сервис позволяет рассчитать расстояние между двумя точками с известными географическими координатами.
Как известно, кратчайшим расстоянием между двумя точками на земной поверхности является длина дуги круга, проведенного на сфере по этим двум точкам. При расчете расстояния по географическим координатам делается предположение, что Земля не плоская, а круглая (если быть точнее, имеет форму, приближенную к сфере), то есть Земля — сфероид.
Для определения расстояния между двумя точками будет применяться формула расчета длины дуги, так называемая «модифицированная формула гаверсинусов».
Поскольку в расчете участвует радиус, а у Земли, как у не совсем правильной сферы, он разный, скажем на северном полюсе — 6335.437 км, а на экваторе — 6399.592 км. В связи с этим в расчете берется среднее значение радиуса Земли равное 6372.795 км, что позволяет получать результат с точность 99,5%.
В калькуляторе ниже для примера приводится расчет расстояния между координатами г.Москва и г.Санкт-Петербург.
Навигатор по конфигурации базы 1С 8.3 Промо
Универсальная внешняя обработка для просмотра метаданных конфигураций баз 1С 8.3.
Отображает свойства и реквизиты объектов конфигурации, их количество, основные права доступа и т.д.
Отображаемые характеристики объектов: свойства, реквизиты, стандартные рекизиты, реквизиты табличных частей, предопределенные данные, регистраторы для регистров, движения для документов, команды, чужие команды, подписки на события, подсистемы.
Отображает структуру хранения объектов базы данных, для регистров доступен сервис «Управление итогами».
Платформа 8.3, управляемые формы. Версия 1.1.0.85 от 10.10.2021
3 стартмани
Алгоритм
Построим алгоритм по общей схеме алгоритмов «разделяй-и-властвуй»: алгоритм оформляем в виде рекурсивной функции, которой передаётся множество точек; эта рекурсивная функция разбивает это множество пополам, вызывает себя рекурсивно от каждой половины, а затем выполняет какие-то операции по объединению ответов. Операция объединения заключается в обнаружении случаев, когда одна точка оптимального решения попала в одну половину, а другая точка — в другую (в этом случае рекурсивные вызовы от каждой из половинок отдельно обнаружить эту пару, конечно, не смогут). Основная сложность, как всегда, заключается в эффективной реализации этой стадии объединения. Если рекурсивной функции передаётся множество из точек, то стадия объединения должна работать не более, чем , тогда асимптотика всего алгоритма будет находиться из уравнения:
Решением этого уравнения, как известно, является .
Итак, перейдём к построению алгоритма. Чтобы в будущем прийти к эффективной реализации стадии объединения, разбивать множество точек на два будем согласно их -координатам: фактически мы проводим некоторую вертикальную прямую, разбивающую множество точек на два подмножества примерно одинаковых размеров. Такое разбиение удобно произвести следующим образом: отсортируем точки стандартно как пары чисел, т.е.:
Тогда возьмём среднюю после сортировки точку (), и все точки до неё и саму отнесём к первой половине, а все точки после неё — ко второй половине:
Теперь, вызвавшись рекурсивно от каждого из множеств и , мы найдём ответы и для каждой из половинок. Возьмём лучший из них: .
Теперь нам надо произвести стадию объединения, т.е. попытаться обнаружить такие пары точек, расстояние между которыми меньше , причём одна точка лежит в , а другая — в . Очевидно, что для этого достаточно рассматривать только те точки, которые отстоят от вертикальной прямой раздела на расстояние, меньшее , т.е. множество рассматриваемых на этой стадии точек равно:
Для каждой точки из множества надо попытаться найти точки, находящиеся к ней ближе, чем . Например, достаточно рассматривать только те точки, координата которых отличается не более чем на . Более того, не имеет смысла рассматривать те точки, у которых -координата больше -координаты текущей точки. Таким образом, для каждой точки определим множество рассматриваемых точек следующим образом:
Если мы отсортируем точки множества по -координате, то находить будет очень легко: это несколько точек подряд до точки .
Итак, в новых обозначениях стадия объединения выглядит следующим образом: построить множество , отсортировать в нём точки по -координате, затем для каждой точки рассмотреть все точки , и каждой пары посчитать расстояние и сравнить с текущим наилучшим расстоянием.
На первый взгляд, это по-прежнему неоптимальный алгоритм: кажется, что размеры множеств будут порядка , и требуемая асимптотика никак не получится. Однако, как это ни удивительно, можно доказать, что размер каждого из множеств есть величина , т.е. не превосходит некоторой малой константы вне зависимости от самих точек. Доказательство этого факта приведено в следующем разделе.
Наконец, обратим внимание на сортировки, которых вышеописанный алгоритм содержит сразу две: сначала сортировка по парам (,), а затем сортировка элементов множества по. На самом деле, от обеих этих сортировок внутри рекурсивной функции можно избавиться (иначе бы мы не достигли оценки для стадии объединения, и общая асимптотика алгоритма получилась бы )
От первой сортировки избавиться легко — достаточно предварительно, до запуска рекурсии, выполнить эту сортировку: ведь внутри рекурсии сами элементы не меняются, поэтому нет никакой необходимости выполнять сортировку заново. Со второй сортировкой чуть сложнее, выполнить её предварительно не получится. Зато, вспомнив сортировку слиянием (merge sort), которая тоже работает по принципу разделяй-и-властвуй, можно просто встроить эту сортировку в нашу рекурсию. Пусть рекурсия, принимая какое-то множество точек (как мы помним, упорядоченное по парам ) возвращает это же множество, но отсортированное уже по координате . Для этого достаточно просто выполнить слияние (за ) двух результатов, возвращённых рекурсивными вызовами. Тем самым получится отсортированное по множество.

Эта тема закрыта для публикации ответов.